Models of Computation | Lecture Notes 4

2016 September 09. Friday.

What is this?

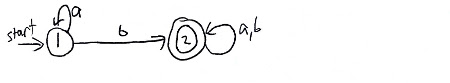
Fall 2016, University of Kentucky, Models of Computation, CS 575, with Dr Goldsmith. These incomplete lecture notes are just my own, not proofread or edited by Dr G or anyone else, so watch out for errors. If you see one then leave a comment or email me.

Algorithm to Turn a DFA into a Regular Expression

Remember or look up deterministic finite automatons (DFA’s), nondeterministic finite automatons (NFA’s), and regular expressions. Today we invent a new finite automaton, the generalized nondeterministic finite automaton (GNFA). It’s like an NFA except a transition arrow can also be labeled as any regular expression.

We’ll use this invention to prove that you can turn any DFA into a regular expression. (“Turn into” means that the regular expression will generate exactly the same strings that the automaton returns accept on.)

Let’s do an example. This is taken from chapter 1 of Theory of Computation by Sipser. Look at this DFA:

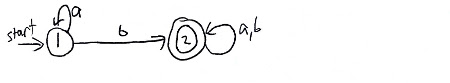
First, make two new states, s and a. Second, make s the new start state and draw an $$ arrow from it to the old start state. Third, turn all the old accept states into reject states, and draw an $$ arrow from each of them to s, and make s an accept state. In this example we only had one original accept state. Fourth, replace all arrows with their regular expression form. In this example, that’s just the a, b arrow turning into an a U b arrow.

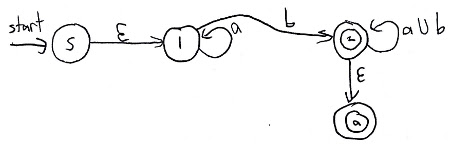
Pluck state number 2, reconnect what’s left behind, and adjust the arrow labels to compensate:

Now pluck state number 1 fill back in:

Now we have a regular expression.

In general, the algorithm works like this and can turn any DFA into a regular expression:

Initial setup. Add s and a. Shift the accept states and start state. Make the arrow labels look like regular expressions.
Pluck off each state one by one and each time fill back in the arrows where you need to.

Last lecture you had an exercise that showed you can turn any regular expression into a DFA. Combining that with this, we now know that regular expressions and DFA’s are completely equivalent.

Step back and look at what we’ve done. Languages, DFA’s…

This has been our first major chunk in Models of Computation.

First, we invented this idea of an alphabet. We said an alphabet is a set of symbols, e.g {a, b, c}.
Then we invented something called a string. We said that a string is zero or more letters in an alphabet stuck together. e.g aaba.
Then we invented a language, a set of strings. e.g {aaba, a, abb}.
Then we invented a deterministic finite automaton (DFA), a robot that will take in a string and either accept or reject it.
Then we invented the adjective regular to describe languages where there is some DFA so that every string in the language is accepted by it and no other strings are accepted.
Then we invented regular expressions, they look something like (a+b)*(aab)*bb.
Then we wanted to show that the set of languages generated by regular expressions is exactly the set of regular languages. We had invented a bunch of things and then we wanted to show something about them. This is how math works.
- To show you can convert a regular expression into a DFA, we invented a nondeterministic finite automaton.
- To show you can convert a DFA into a regular expression, we invented the generalized nondeterministic finite automaton (GNFA).

Now we know that regular languages and DFA’s are the same. This is our first major result. Get ready for more as the class goes on.

Properties of Regular Languages

If $L$ is regular, then $L$ (read as $L$ complement) is also regular.

(This is also stated “The class of regular languages is closed under complement.”)

Why?

Well if $L$ is regular, then there is a DFA that accepts exactly $L$. If I copy that DFA but make all the reject states into accept states and make all the accept states into reject states, then my new DFA will accept everything but $L$.

Here is a DFA that accepts L = ((a U b) b* a)*:

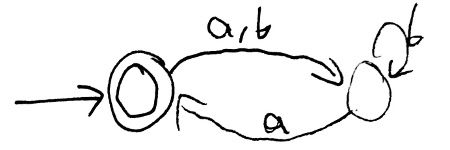
Here is a DFA that accepts $L$

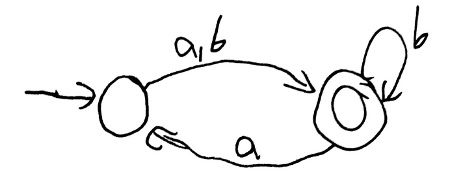
Note that flipping the accept and reject states works for a DFA but not for an NFA. I encourage you to do an example or two and see why not.

The class of regular languages is also closed under + * (star), + concatenation, + union, + complement, and + intersection.

Note that the last one, intersection, isn’t trivial. We’ve seen union using epsilons in an NFA, but intersection requires you to cross-product two DFA’s.

Sidenote: The Pigeon Brain Principle

If you are in an elevator with n people, and m > n buttons have been pushed, then at least one person pushed at least two buttons.

Mathematically, we say a function

$f: \{0, 1, \dots, n\} \to \{0, 1, \dots, n, n+1\}$

can never be one-to-one.

So, if you have a DFA with n states, and you give it a string of length m > n, then at least one state must be visited at least twice.

More generally, the pigeon brain principle is hugely useful in mathematics and many major theorems rely on it.

Exercise

Look at this language:

$L = \{ a^n b^n : n \in \mathbb N \} = \{ \epsilon, ab, aabb, aaabbb, \dots \}$

Is it regular? If it is then draw me the DFA. If it’s not then explain why not.

And that’s lecture.

Public Domain Dedication.