
Judy Goldsmith is a professor at the University of Kentucky. In fall 2016 she is teaching a class called Models of Computation. Here’s what she talked about today…
(These notes were not proofread or edited by Dr Goldsmith or anyone, so they probably have lots of mistakes.)
{a,b} that have an even number of a’s and an odd number of b’s.**DFA stands for Deterministic Finite Automaton. Really it is just faces and arrows and letters. You give it a string (a sequence of letters, like thefishisgood) and it will either accept or deny that string. Here we are only using the letters a and b, so a string looks like abaab.
Here is one DFA, it will accept an even number of a’s and it doesn’t care about b’s:

Let’s run it on abaab. It starts on smiley, then then the first a moves it to frowny, then the b loops to frowny, then a moves it to smiley, then a moves it to frowny, then b loops to frowny. The DFA ends on the frowny face so the string abaab is not accepted.
That was a DFA that accepts only strings over {a, b} with an even number of a’s. Here is one that accepts only an odd number of b’s:
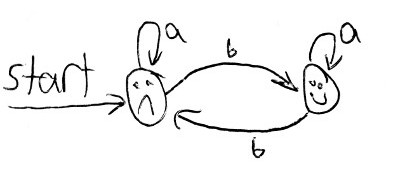
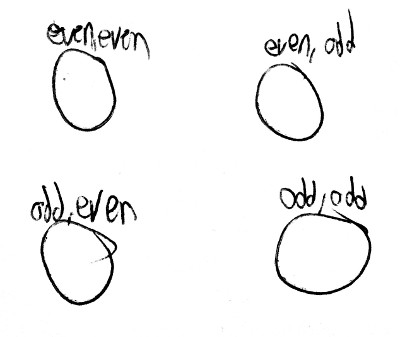
Now let’s think about what a machine that cares about a and b will look like. We need to know whether a is even or odd, and whether b is even or odd. Keeping each of those values in memory is like having two bits, so we need four states to keep track of it all.
And just connect the arrows
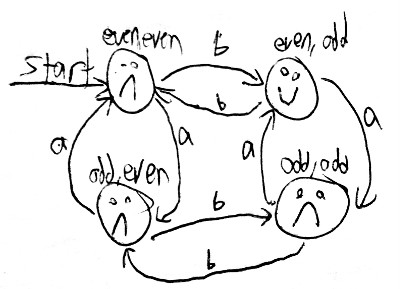
That’s an answer. Check it with a few strings, it will only give a smiley if the string has an even number of a’s and an odd number of b’s.
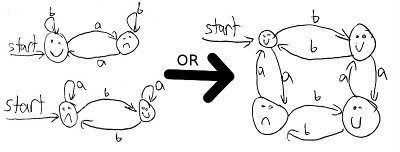
If you look then you’ll see that it is really just the first automoton and’d together with the second. You can also or them together to get an automoton that accepts any string with even a’s or odd b’s.
Last week we talked about an infinite hotel. There are infinity rooms, numbered 1, 2, 3, ... Each room has a guest in it. A new guest shows up and wants a room. You can fit her in, just move guest 1 to room 2, guest 2 to room 3, guest 3 to room 4… Each current guest is just momentarily displaced and the new guest gets room 1.
What if infinity guests show up and each want a room?
Move every n’th guest to the 2xn’th room. Now all the odd numbered rooms are empty, put your guests there.
For next lecture: You have infinity buses show up, each with infinity passengers, everyone needs a room, and your infinite hotel is presently full. Can you fit them all?
(This is slightly different from what Goldsmith said, but I like this one more.)
Last week we gave the following proof:
Consider a computer science class with n students. We will use induction to prove that all students in the class are from the same country.
Clearly, in any set of 1 students, everyone is from the same country.
Now spoze you have a set of k students where everyone is from the same country. Pick one student, Isabel. Kick her out. Now your class has k-1 people in it. Now add anyone from the university to your class. You have k people again, so clearly he must be from the same country as everyone else. Now add Isabel back. k+1 people again, all from the same country.
Therefore, in any class of any size, everyone is from the same country.
What’s wrong with this proof?
It fails when going from 1 student to 2 students. When k=1, k-1=1-1=0 and a “for all” statement fails on an empty set.
Remember that an alphabet is a set of letters.
What is in the set of regular expressions over an alphabet E? (definition)
~, the empty string, is a regular expressionx in E, x is a regular expressionAnd recursion! For all regular expressions u and v
uv (u concatenated with v) is a regular expressionu+v (u or v) is a regular expressionu* (u repeated any number of times) is a regular expressionExamples? If your alphabet is E = {a, b}, then…
b* = {~, b, bb, bbb, bbbb, ...}b’s)(ab)* = {~, ab, abab, ababab, abababab, ...}ab’s)(a+b)* = {~, a, b, aa, ab, ba, bb, aaa, aab, aba, abb, ...}((a+b)(a+b))* = {~, aa, ab, ba, bb, aaaa, aaab, aaba, aabb, abaa, ...}(a*)+(b*) = {~, a, b, aa, bb, aaa, bbb, aaaa, bbbb, ...}a’s or any number of b’s)And that’s lecture.
Public Domain Dedication.